Soros és párhuzamos kapcsolások

Ellenálláshálózatok

Az előző fejezetekben az ellanállást diszkrét alkatrészként tárgyaltuk. A gyakorlatban azonban az ellenállásokat általában egymással vagy más elemekkel összekapcsolva alkalmazzuk.

Az ellanállások összekapcsolásának két alapvető formája létezik: a soros és a párhuzamos kapcsolás.

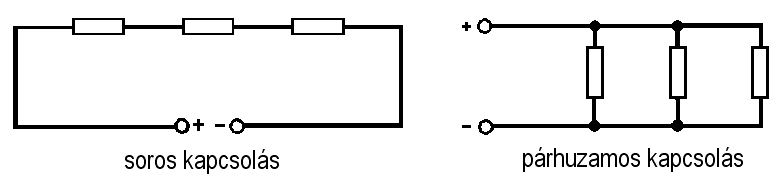
1. ábra : Ellenálláshálózat (soros, párhuzamos)

Sorosan kapcsolt ellenállások

Ha két ellenállásnak csak az egyik vége van összekötve, és közéjük semmi más nem kapcsolódik, akkor a két elem sorba van kapcsolva. Az első elem kezdetére és az utolsó ellenállás végére kapcsolódik a tápfeszültség.

Ismétlésként: Ha egy áramerősség-mérőt iktatunk be bárhová az áramkörbe, akkor az mindenhol ugyanazt az értéket fogja mutatni. (2. ábra)

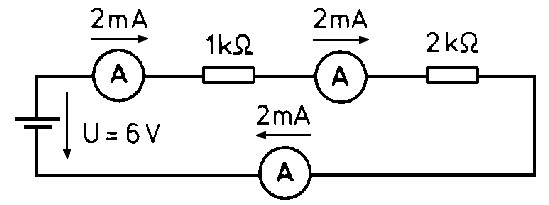
2. ábra: Az áramkörben az áramerősség mindnehol egyenlő

Mivel minden ellenálláson ugyanaz az áram folyik keresztül, így az elemeken létrejövő feszültségesés az Ohm-törvény segítségével könnyen meghatározható.

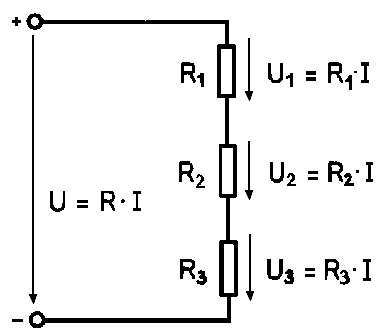
3. ábra: Feszültésgesés a soros ellenállásokon

A teljes tápfeszültség az áramkör eredő ellenállásával áll kapcsolatban :

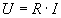
Az ellenállásokon eső feszültésgek összege a tápfeszültséggel egyezik meg (lásd: rádióamatőr vizsgafelkészítő 1. rész 1. lecke)

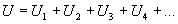
Ha behelyettesítjük a 3. ábrán látható kifejezést a képletbe (U=R*I, U[1]=R[1]*I stb.), akkor a következőt kapjuk:

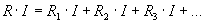
Az áramerősség (I) mindenhol egyenlő, tehát kiemelés után egyszerűsíthetünk vele. Így kapjuk meg a sorosan kapcsolt ellenállások eredőjének kiszámítási módját:

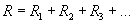
Jegyezzük meg:A sorosan kapcsolt ellenállások összege egyenlő az eredő elenállással.

Példa: három, egyenként 500 Ω-os, 1 kΩ-os és 1,5 kΩ-os ellenállást kapcsolunk sorba és 6 V feszültséget adunk rájuk. Mekkora az eredő ellenállás, az áramerősség és az egyes ellenállásokra eső feszültség?

Adott tehát: R₁ = 500 ohm = 0,5 kΩ, R₂ = 1 kΩ, R₃ = 1,5 kΩ, U = 6 V. Keressük a következőket:

• a) eredő ellenállás (R),
• b) áramerősség (I), I
• c) feszültség az ellenállásokon (U₁, U₂, U₃).

Megoldás: a kapcsolás a 3. ábrán látható

a) R = R₁ + R₂ + R₃
R = 0,5 kΩ + 1 kΩ + 1,5 kΩ
R = 3 kΩ

b)

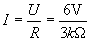
c) U₁ = R₁ * I = 0,5 kΩ * 2 mA = 1 V
U₂ = R₂ * I = 1 kΩ * 2 mA = 2 V
U₃ = R₃ * I = 1,5 kΩ * 2 mA = 3 V.

Ellenőrzésképpen: 1 V + 2 V + 3 V = 6 V

Jegyezzük meg: az ellenállásokot eső feszültségek összege a kapcsolásra jutó teljes feszültséget adja ki.

A feszültségosztó

Az előző számítás alapján egy fontos képletet vezethetünk le.

Jegyezzük meg, hogy soros kapcsolás esetén az egy ellenállásra eső feszültség arányos az ellenállással.

Képletként felírva:

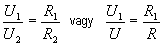
A példában az ellenállások így arányultak egymáshoz:

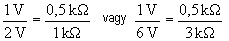
Láthatjuk, hogy kétszeres ellenálláson kétszer akkora feszültség esik.

Jegyezzük meg következő gyakorlati szabályt: nagy ellenálláson nagy a feszültségesés, kicsi ellenálláson pedig kicsi.

A feszültségosztó az ellenállások soros kapcsolásának egyik legfontosabb alkalmazása. Nagyon sokszor azért alkalmazzuk, hogy meghatározott feszültséget állítsunk elő (ld. a TD504 vizsgakérdést)

Ha például egy feszültség túl nagy egy mérőműszer vagy egy relé számára, akkor azt egy előtétellenállással csökkenthetjük. (ld. a TJ501 vizsgakérdést)

TJ501: Egy feszültségmérővel 20 Voltig szeretnénk mérni. A műszer végkitéréséhez 2 V tartozik, ekkor 2 mA folyik át rajta (4. ábra). Mekkora előtétellenállásra van szükség?

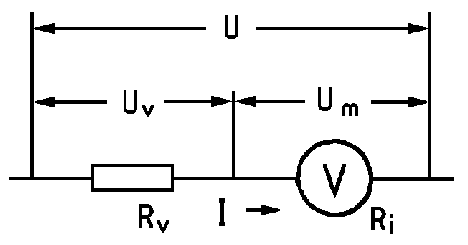
4. ábra: Feszültségmérő méréshatárának kiterjesztése

Adott: U_m = 2 V (U_mm = 2 mA, U = 20 V. Keresett: RV.

Megoldás: U = UV + Um, UV = U - Um, UV = 20 V - 2 V = 18 V.

Az előtétellenálláson 18 V-nak kell esnie. Az Im áram átfolyik az RV előtétellenálláson is.

Ohm törvénye szerint:

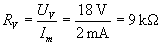
Párhuzamosan kapcsolt ellenállások

Párhuzamos kapcsolásnak azt nevezzük, amikor az alkatrészek azonos végüknél vannak összekötve (5. ábra).

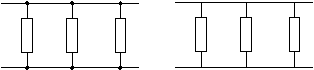
5. ábra: Párhuzamosan kapcsolt ellenállások

Fontos: a vezetékek csomópontját általában nem jelölik, ha a vezetékek nem keresztezik egymást.

Gyakorlat: egy 1 kΩ-os, egy 2 kΩ-os és egy 3 kΩ-os ellenállást kössünk párhuzamosan és kapcsoljunk rájuk U = 6 V feszültséget. Mérjük meg az összes ágban folyó áramot és a teljes áramot.

A 6. ábrán szereplő értékeket kell kapnunk.

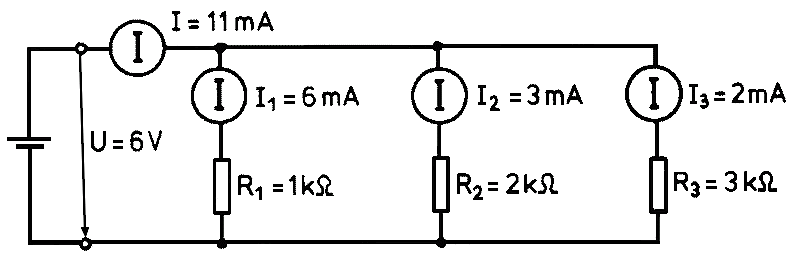
6. ábra: Párhuzamosan kapcsolt ellenállások mérési elrendezése és mérési eredményei.

A kísérlet eredményei alapján a következő törvényszerűséget vonhatjuk le.

Párhuzamos kapcsolásnál minden ellenálláson ugyanakkora feszültség esik.

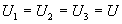
Jegyezzük meg: a teljes áram a ágak áramainak összege.

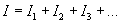
És ami első ránézésre talán nem nyilvánvaló, bár rövid utánaszámolással ellenőrizhető, az a következő törvényszerűség:

Jegyezzük meg: Az áramok az ellenállások értékeivel fordítottan arányosak.

Két példa a 6. ábráról:

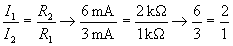
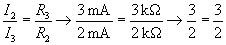
A párhuzamosan kapcsolt ellenállások eredőjének levezetését itt mellőzzük, az eredmény a következő:

Szavakkal kifejezve: párhuzamos kapcsolás esetén az ellenállások reciprokai adódnak össze. Az ellenállás reciprokát vezetésnek is nevezzük.

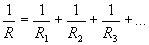
Szavakkal kifejezve: párhuzamos kapcsolás esetén az ellenállások reciprokai adódnak össze. Az ellenállás reciprokát vezetésnek is nevezzük.

Jegyezzük meg: a párhuzamos kapcsolás eredő vezetése az egyes ellenállások vezetésének összege.

A TD500 vizsgakérdésben adott három párhuzamosan kapcsolt ellenállás eredője és kettő értéke. Kérdés: mekkora R3? A megoldáshoz fejezzük ki 1/R3-t a fenti képletből:

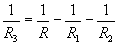
Az eredő ellenállás adott: 1,66 kΩ. R1 értéke 3,3 kΩ, R2-é 5,6 kΩ. R3-t kell ezek ismeretében kiszámítani. Ez a legegyszerűbben a következőképpen tehetjük meg: először is behelyettesítjük a számértékeket, a kiloohm nélkül.

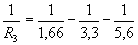
Ezután a zsebszámológéppel így számolok tovább: beírom az 1,66-ot, veszem a reciprokát ("1/x" gomb), "-" gombot nyomok, jön az 3,3, újra "1/x", aztán "-", végül 5,6, "1/x", ezután a "=" gombot nyomom meg, és végül pedig ismét az "1/x"-t. Ekkor 8,2776039 jelenik meg a képernyőn, ami kb. 8,3 kΩ-ot jelent. Ez az eljárás kicsit talán bonyolultnak tűnik, de az egyes lépéseket a képlettel összevetve könnyen megérthető.

Ha csak két ellenállást kapcsolunk párhuzamosan, akkor az eredő ellenállást másképpen is felírhatjuk. Rendezzük át az eredő ellenállás képletét:

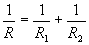
úgy, hogy a baloldalon R álljon. Ezt kell kapnunk:

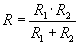
Példa: egy 20 Ω-os és egy 30 Ω-os ellenállást kapcsolunk párhuzamosan. Mekkora az eredő ellenállás?

Megoldás:

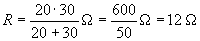
Amennyiben n darab egyforma ellenállást kapcsolunk párhuzamosan, akkor az eredő egy ellenállás értének n-es része lesz.

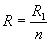
Példa: négy 2 kΩ-os ellenállást kapcsolunk párhozamosan. Mekkora az eredő ellenállás?

Megoldás:

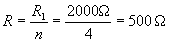
Ellenállások vegyes kapcsolása

A gyakorlatban legtöbbször részben sorba és részben párhuzamosan kapcsolt ellenállásokkal találkozuk, ezeket általában vegyesen kapcsoltnak nevezzük.

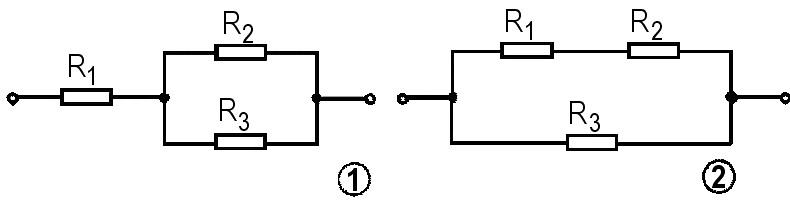
7. ábra: Két egyszerű vegyes kapcsolás.

Az 1-es áramkörben az R2 és R3 párhuzamosan kapcsolódik, velük sorba pedig az R1. Az 2-es áramkörben az R1 és R2 soros kapcsolásához van az R3 párhuzamosan kötve. Ezek alapján a következő példákat nem nehéz megoldani.

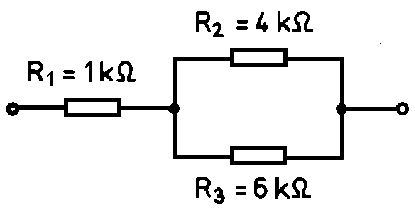
8. ábra: Példa a 7. ábra 1-es kapcsolására.

Elsőként R2 és R3 párhuzamos eredőjét számítjuk ki.

[Image126.gif] kΩ egységekben

R2/3 = 2,4 kΩ

Ehhez kapcsolódik a soros ellenállás: Rges = 1 kΩ + 2,4 kΩ = 3,4 kΩ

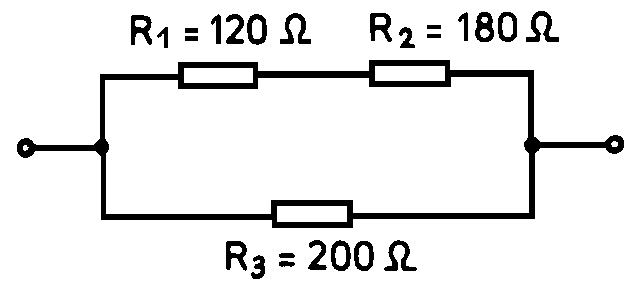
9. ábra: Példa a 7. ábra 2-es kapcsolására.

Először R1 és R2 soros eredőjét számítjuk ki: R1/2 = 120 Ω + 180 Ω = 300 Ω

Ezzel kapcsolódik sorba R3:

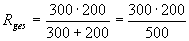
Rges = 120 Ω.

Összefoglalás

Soros kapcsolás

• Az áram midenhol azonos.
• A ellenállásokon eső részfeszültségek összege megegyezik a teljes feszültséggel.
• A részfeszültségek arányosak az ellenállásokkal.
• Az eredő ellenállás az ellenállások összege.
• Alkalmazás: feszültségmérő méréshatárának kiterjesztése.

Párhuzamos kapcsolás

• A feszültség mindenhol azonos.
• A ágakban folyó részáram összege a megegyezik a teljes árammal.
• A részáramok fordítottan arányosak az ellenállásokkal.
• Az eredő vezetés az vezetések összege.
• Alkalmazás: árammérő méréshatárának kiterjesztése.

Vizsgakérdések

TD500 Három párhuzamosan kapcsolt ellenállás eredője 1,66 kΩ. R1=3,3 kΩ, R2=5,6 kΩ. Mekkora R3?

• a) 8,3 kΩ
• b) 9,2 kΩ
• c) 10,6 kΩ
• d) 8,9 kΩ

TD501 Két párhuzamosan kapcsolt ellenállás aránya R1 : R2 = 1 : 2 . R2-n 50 mA áram folyik. Mekkora áram folyik R1-en?

• a) 100 mA
• b) 25 mA
• c) 200 mA
• d) 66,6 mA

TD502 Mekkora a kapcsolás eredő ellenállása?

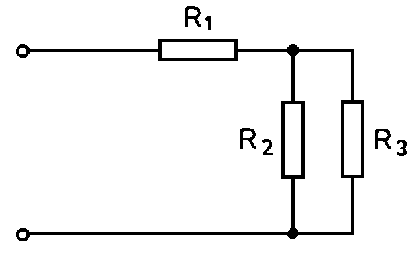
• a) 1000 Ω
• b) 2500 Ω
• c) 1500 Ω
• d) 250 Ω

TD503 Mekkor a TD502 kérdésben szereplő kapcsolás eredő ellenállása, ha R1 = 3,3 kΩ, R2 = 4,7 kΩ, R3 = 27 kΩ ?

• a) 7,3 kΩ
• b) 4,0 kΩ
• c) 1,8 kΩ
• d) 35 kΩ

TD504 Milyen arányban oszlik meg a feszültség a két ellenálláson, ha R1 5-ször akkor, mint R2?

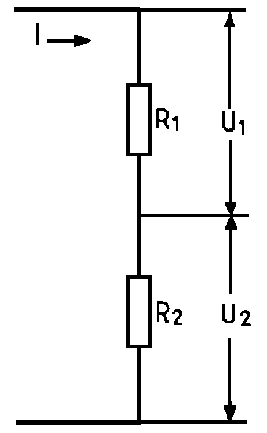
• a) U1 = 5 · U2
• b) U1 = 6 · U2
• c) U1 = U2 / 5
• d) U1 = U2 / 6

TJ501 Mekkora Rv előtétellenállásra van szükség ahhoz, hogy egy 2 V végkitérésű műszert mérési tartományát 20 V-ra növeljük? Teljes kitérésnél a műszeren 2 mA áram folyik.

• a) Rv = 9 kΩ
• b) Rv = 10 kΩ
• c) Rv = 90 kΩ
• d) Rv = 0,1 MΩ

Hinweis

Die richtigen Lösungen der Prüfungsfragen finden Sie auf der Homepage unter [4]ANHANG

Prüfungsfragen-Test

Sie können sich selbst testen, indem Sie in folgender Tabelle auf die einzelnen Fragen klicken. Denken Sie aber an Ihre Telefonkosten, wenn Sie online sind! Um Online-Telefonkosten zu sparen, wird es in Kürze die komplette Homepage [5]www.amateurfunkpruefung.de auf CD ROM geben. Schauen Sie diesbezüglich auf die private [6]Homepage von DJ4UF.

[7]TD500 [8]TD501 [9]TD502 [10]TD503 [11]TD504 [12]TJ501

© http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:34
Eredeti mű: © Eckart Moltrecht DJ4UF, http://www.amateurfunkpruefung.de