Egy kis matematika

Ez a fejezet nem tartozik szorosan a Rádióamatőr vizsga témaköréhez, azonban a későbbi elektrotechnikai alapok könnyebb megértése miatt néhány alap mértékegységgel és néhány képlettel illetve alapvető képleten végezhető átalakításokkal célszerű tisztában lennünk.

Alapegységek és mennyiségek

A Nemzetközi Mértékegység-rendszert (SI) az 1875-ös Méteregyezményre alapozva, a méterrendszer 1948-ban elhatározott kiterjesztéseként a 11. Általános Súly- és Mértékügyi Értekezlet részvevői 1960-ban fogadták el. (Magyarországon az SI mértékegység rendszer 1976. óta hatályos. [8/1976. (IV. 27.) MT számú rendelet.]). Az SI mára világszerte közös része az aláíró országok hivatalos mértékegységeinek.

A Nemzetközi Mértékegység-rendszer hét, egymástól függetlennek tekintett alapmennyiség egységeiből úgy épül fel, hogy az alapmennyiségekből származtatott mennyiségek egységeit ugyanazon összefüggések segítségével származtatják az alább látható alapmennyiségek egységeiből, mint az illető mennyiségeket (koherencia).

Alapegység Mértékegység Jele

hosszúság méter m

tömeg kilogramm kg

idő másodperc s

áramerősség amper A

hőmérséklet kelvin K

anyagmennyiség mol mol

fényerő candela cd

Ebben a tananyagban csak az első négy alapegységet: hosszúság, tömeg, idő és áramerősség fogjuk bemutatni.

A mértékegység-rendszer használatát egy példán keresztül mutatjuk be. A következő matematikai kifejezést szeretnénk leírni: a huzalantenna hosszúsága 41 méter. Ebben az esetben a kívánt érték az alábbi formában írható le:

l = 41 m

Feladat
Írjuk fel a következő matematikai egyenletet: Az áramerősség 2,5 amper.

Megoldás: I = 2,5 A

A mértékegységekkel az értékek ismerete nélkül, például az értékek későbbi beírásával, is végezhetünk matematikai műveletet.

Képletek átalakítása

A tanfolyam első fejezetében a következő összefüggéseket ismerhetjük meg: egységnyi felületre (A) jutó áramsűrűség (S) a következő képlettel írható fel:

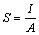
A képletben szereplő A a felület, az I az áramerősség, a kettő hányadosa azaz az egységnyi felületre jutó áramerősség az S, amit áramsűrűségnek nevezünk. Az SI mértékegysége az A/mm²

Számítási példa

Egy vizsgakérdésben például a következő szerepel: az ismert felület nagysága 0,196 mm² Mekkora a legnagyobb megengedhető áramerősség, ha az áramsűrűség értéke 2,5 A/mm².

A számításhoz a fenti képlet segítségével ki kell számítanunk az áramerősséget I .

Egyszerű törtek esetében nézzük meg, hogy szerepel-e a keresett mértékegység a tört számlálójában vagy nevezőjében.

A tört számlálójában (fent) szerepel, ezért az egyenlet mindkét oldalát megszorozzuk a nevezőben szereplő mértékegységgel, jelen esetben A-val.

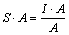
Az egyenlet jobb oldalán lévő A ezáltal kiesik, és marad

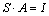
vagy írhatjuk fordítva is

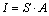
Az értékek behelyettesítésével a következő egyenletet írhatjuk fel

Összefoglalva: 0,196 mm² keresztmetszetű vezetékkel, maximum 2,5 amper/mm² áramsűrűség mellett az átvezetendő áram erőssége nem haladhatja meg a 0,49 ampert.

Abban az esetben, ha a keresett mértékegység a tört nevezőjében szerepel, még egy lépésre szükségünk van a képlet felírásához.

Számítási példa

Azt szeretnénk meghatározni, hogy mekkora keresztmetszetű vezetékre lenne szükségünk, ha 0,49 A áramot szeretnénk elvezetni és a megengedhető legnagyobb áramsűrűség 2,5 A/mm².

A képletet A-ra kell felírnunk.

A keresett értékne a tört számlálójában történő megjelenéséhez az egyenlet mindkét oldalát meg kell szoroznunk A-val.

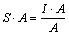
Az egyenlet jobb oldalán szereplő A kiesik, továbbá az egyenlet bal oldalán lévő S-re nincs szükségünk, ezért mindkét oldalt osszuk el S-sel.

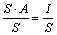
Az S kiesik és a következő eredményt kapjuk

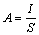
Ellenőrizzük az eredményt, az értékek beírásával!

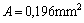
Ohm-törvény képlet átalakítások

Gyakran találkozhatunk az Ohm-törvényre felírható képlettel: U = R * I
vagy a teljesítmény kiszámításához alkalmazott képlettel: P = U * I

amely képletekben a három mértékegység közül az egyikre írjuk fel az egyenletet. Matematikailag ez úgy néz ki, hogy az egyenlet mindkét oldalát azzal a mértékegységgel osztjuk el, amelyikre nincs szükségünk az egyenlet megoldásához.

Például P = U * I egyenletet I-re szeretnénk felírni. Osztunk U-val, ezért az egyik oldalon marad egy felesleges I .

Azok, akik nehezen boldogulnak a képlettel, a következő segítséget használhatják. A képlet egy háromszögbe is felírható

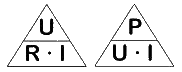
1. ábra: URI- és PUI-háromszög

A háromszöget a következőképpen használhatjuk.

Az Ohm-törvény esetében az áramerősség kiszámításakor, takarjuk le az I betűt és a maradék, látható betűkből megkapjuk a szükséges képletet.

A vízszintes vonal osztásnak felel meg. Tehát ebben az esetben:

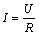
Feladat: Próbáljuk meg a P = U * I képletet osztással és szorzással átalakítgatni, és figyeljük meg, hogyan tudjuk kifejezni belőle az U-t, az I-t és a P-t.

A négyzetre emelés, gyökvonás, összegek, különbségek képleteit a B vizsgára felkészítő tananyag első fejezetében fogjuk gyakorolni.

Tíz hatványai

Mérési eredményeknél a kapott értékek lehetnek egy egység többszörösei, vagy részei. Többnyire a mértékegységek decimális többszöröseit, vagy részeit használjuk, például kilo = ezerszeres vagy milli = ezred rész.

Tényező Hatvány Mértékegység Rövidítés

billioszoros 10¹² tera T

milliárdszoros 10⁹ giga G

milliószoros 10⁶ mega M

ezerszeres 10³ kilo k

százszoros 10² hekto h

tízszeres 10¹ deka da

tized 10^-1 deci d

század 10^-2 centi c

ezred 10^-3 milli m

milliomod 10^-6 mikro µ

milliárdod 10^-9 nano n

billiomod 10^-12 piko p

A tera, giga és mega rövidítéseket mindig nagybetűvel, a betűket és minden mást kisbetűvel kell írni. Különösen fontos az m vagy M (milli vagy Mega) és a k = kilo esetében, a nagy K a digitális technikában (Kilo) használatos, ahol K = 1024 1 Kilobyte (1 KB) = 1024 Byte.

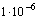
ugyanazt jelenti mint:

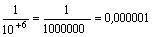
A hatványkitevőt a következőképen határozhatjuk meg: az egynél kisebb számok esetében a tizedesvesszőtől jobbra eső utolsó számig számolunk, ha a példában szereplő utolsó szám a második helyen szerepel (0,42), 10, ha a harmadik helyen szerepel (0,042) 10^-3 és így tovább, majd a nullák elhagyásával kapott számot leírva 42-t kapunk. Például:

0,42 = 42×10^-2 vagy
0,042 = 42×10^-3 vagy
0,00042 = 42×10^-5

Megjegyzés: A következőkben az EM rövidítés Eckart Moltrecht-et jelent. Az „EM”-mel jelölt kérdések csak a szerző által kitalált kérdések, feladatok.

Feladatok

Gyakorló feladat EM001: Hogy írhatjuk másképpen a 0,042 A-t?

a) 42×103 A b) 42×10^-2 A
c) 42×10^-1 A d) 42×10^-3 A

Célszerű a mértékegységeket (kilo, milli, mikro,stb.) átváltani, ha az értékek kitevői a következőképpen vannak megadva pl.: 3 (kilo), 6 (Mega), 9 (Giga) vagy -3 (milli), -6 (mikro), -9 (nano) vagy -12 (piko).

Az utolsó helyiértéken szereplő számok esetében, az utolsó számhoz írhatunk egy nullát is anélkül, hogy az a mennyiség értékét megváltoztatná. Például 0,00042 esetében 0,000420. Most az utolsó számjegyig 6-ot kell számolnunk, tehát 10-6 leírva: 420×10-6.

Gyakorló feladat EM002: Fejezzük ki másképpen a 0,00042 A-t!

a) 420×10^-6 A b) 420×10⁶ A
c) 420×10^-5 A d) 42×10^-6 A

A számokat úgy fejezhetjük ki hatványkitevős alakban, hogy az utolsó helyiértéktől addig visszük balra a tizedesvesszőt, amíg a tizedesvessző baloldalán közvetlenül csak egy nem nulla számjegy lesz. Amennyivel a tizedesvesszőt balra vittük, az a szám lesz a kitevő értéke.

Például:

420 = 420,0 = 4,200×10² = 4,2×10²
4200 = 4,2×10³
42000 = 4,2×10⁴

Gyakorló feladat EM003: Fejezük ki másképpen a 4 200 000 Hz-et

a) 42×10^-5 Hz b) 4,2×10⁵ Hz
c) 42×10⁶ Hz d) 4,2×10⁶ Hz

Fordított esetben, ha például egy hatványkitevős számot szeretnénk decimálisan kifejezni, a következőképpen járunk el. A tizedesvesszőt annyi helyiértékkel visszük jobbra, amennyi a kitevőben szerepel.

Például

5,1×10² = 510
51 ×10⁵ = 5100000

Gyakorló feladat EM004: Az 510×10²

a) 5100 b) 51000
c) 0,0051 d) 0,051

Gyakorló feladat EM005: Az 51×10⁴

a) 510000 b) 51000
c) 0,00051 d) 0,000051

Ellenőrzésképpen hasonlítsuk össze a kapott értékeket a fenti táblázatban szereplő értékekkel!

Gyakorló feladat EM006: Írjuk fel másképpen: 0,22 µF

a) 220 nF b) 22 nF
c) 220 pF d) 22 pF

Megoldás: Az érték átváltásakor a következőképpen járhatunk el: a µ felírhatjuk 10^‑6 képpen, tehát a tizedesvesszőt hat helyiértékkel kell balra vinnünk:

0,22 µF = 0,000000220 F

Az üres helyiértékek helyére írjunk nullákat! Az így kapott szám esetében a tizedesvessző után kilenc szám szerepel, tehát a kapott mértékegység nano lesz, amit úgy írhatunk fel, hogy 220 nF.

Gyakorló feladat EM007: Írjuk fel másképpen: 0,047 kW

a) 47 MW b) 470 W
c) 47 W d) 470 mW

Gyakorló feladat EM008: Írjuk fel másképpen: 144250 kHz

a) 0,14425 MHz b) 14,425 MHz
c) 1,4425 MHz d) 144,25 MHz

Gyakorló feladat EM009: Írjuk fel másképpen: 3,75 MHz

a) 375 kHz b) 3750 kHz
c) 0,0375 GHz d) 0,375 GHz

Gyakorló feladat EM010: Írjuk fel másképpen: 0,022 A

a) 22 µA b) 220 µA
c) 22 mA d) 220 mA

Vizsga feladat TA113: Írjuk fel másképpen: 100 mW

a) 0,01 W b) 0,001 W
c) 10^-1 W d) 10^-2 W

Gyakorló feladat EM011: Az eddig tanultak alapján írjuk be a táblázat hiányzó részeibe a helyes megoldásokat.

U = 1280 volt U = 1,28 kV

I = 0,038 amper I =_____ mA

f = 3580 kilohertz f =____ MHz

P = ______ watt P = 450 mW

R = 27000 ohm R =____ kW

U = 0,00001 volt U = ____ V

I = 0,00025 amper I =_____ mA

R = 0,047 megaohm R = ___ kW

t = 0,00005 másodperc t = _____ s

Megoldások

EM001 d EM002 a EM003 d EM004 b
EM005 a EM006 a EM007 c EM008 d
EM009 b EM010 c TA113 c

EM011 Gyakorló feladat megoldása:

U = 1280 volt U = 1,28 kV

I = 0,038 amper I = 38 mA

f = 3580 kilohertz f = 3,58 MHz

P = 0,45 watt P = 450 mW

R = 27000 ohm R =27,0 kΩ

U = 0,00001 volt U = 10 V

I = 0,00025 amper I = 0,25 mA

R = 0,047 megaohm R = 47,0 kΩ

t = 0,00005 másodperc t = 50 s

© http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:33
Eredeti mű: © Eckart Moltrecht DJ4UF, http://www.amateurfunkpruefung.de