Rezgőkörök és szűrők
A nagyfrekvenciás technikában, és így az amatőr rádiótechnikában is nagyon fontos szerepe van a rezgőkörnek, amely egy tekercs és egy kondenzátor összekapcsolásával jön létre. Megkülönböztetjük a soros és a párhuzamos rezgőkört, ami egy tekercs és egy kondenzátor soros illetve párhuzamos kapcsolása (1. ábra).
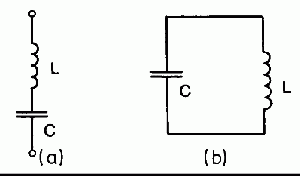
1. ábra: (a) Soros rezgőkör, (b) párhuzamos rezgőkör.
A rezgés menete
A két áramköri elemben - a tekercsben és a kondenzátorban - az a közös, hogy képesek energiát felvenni, amit később le is tudnak adni.
A kondenzátornak elektromos energiára van szüksége az elektromos erőtér felépítéséhez (a kondenzátor feltöltéséhez), ami aztán a kisülésnél felszabadul. Ugyanígy a tekercsnek is szüksége van elektromos energiára, de ebben az esetben ez a mágneses erőtér felépítéséhez kell. A mágneses erőtér megszűnése közben ez az energia szabadul fel. Ez különösen jól megmutatkozik például a relétekercseknél, ahol a szabaddá váló energia a megszűnő érintkezésnél szikrát hoz létre.
Ha ezen összekapcsolt áramköri elemek bármelyikével energiát közlünk - például egy kondenzátor kívülről bevezetett töltésével -, akkor az energia elkezd "ingázni" a két áramköri elem között. A tekercs és a kondenzátor felváltva működik energiaforrásként és energiatárolóként.
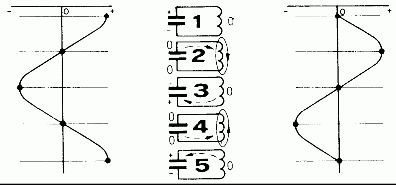
2. ábra: A rezgőkörben az energia a kondenzátor (balra) és a tekercs (jobbra) között ingázik oda-vissza.
Ha (legalábbis gondolatban) egy feltöltött kondenzátort egy tekercsre kötünk (lásd a 2. ábrán az 1. fázist), akkor a kondenzátor a tekercsen keresztül kisül. Ezalatt a tekercsben az áram miatt mágneses erőtér jön létre, amíg az elektromos tér a kondenzátorban megszűnik.
A kisülési folyamat végén az összes energia mágneses erőtér formájában a tekercsben van. Ahogy megszűnik az áram (2. fázis), a mágneses erőtér elkezd összeomlani, és az ez által indukált feszültség áramot indít, ami által a kondenzátor ellentétes irányban ismét feltöltődik.
Ha a rezgőkörnek nem lenne vesztesége, akkor most az összes energia újra a kondenzátorban lenne (3. fázis), és most az egész folyamat ellentétes irányban ismét lezajlana (4. ás 5. fázis). Ennek az eredménye egy csillapítatlan rezgés lenne (3. ábra).

3. ábra: Csillapítatlan és csillapított rezgés (csillapítatlan, gyengén csillapított, erősen csillapított).
De mivel minden tekercsnek van ohmos ellenállása (rézdrótból készül!), a rezgési folyamat közben mindig egy kevés energia hővé alakul, ami miatt a rezgés amplitudója folyamatosan csökken. Ezt nevezik a rezgés csillapodásának. Ha csillapítatlan rezgést akarunk létrehozni (pl. egy adóhoz), akkor a megfelelő időpillanatban kívülről pótolni kell a rezgőkör hiányzó energiáját.
A rezonanciafrekvencia
Az egy teljes rezgéshez szükséges idő a kapacitás és az induktivitás nagyságától függ. Ha például nagyon nagy a kapacitás, akkor sok időt vesz igénybe a kondenzátor kisülése. Tehát a rezgés frekvenciája nagyon kicsi lesz (2. ábra).
A legnagyobb amplitúdójú rezgés akkor áll elő, ha az X_C kapacitív ellenállás és az X_L induktív ellenállás azonos értékű. Ezt az állapotot nevezzük rezonanciának.
A következő összefüggésből
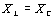
ki lehet számolni azt a frekvenciát, ahol ez a feltétel teljesül. Az eredmény:

Ez a Thomson képlet, amely az Ohm törvény után a második legfontosabb a rádióamatőr számára.
A soros rezgőkör
Ha egy tekercset és egy kondenzátort sorba kapcsolunk, akkor egy soros rezgőkört kapunk (4. ábra).
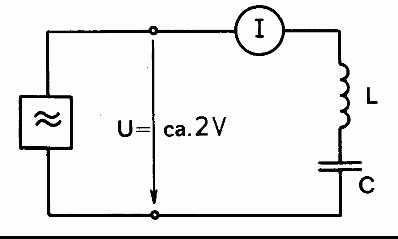
4. ábra: Váltófeszültségű generátorral táplált soros rezgőkör.
Kísérlet
Ha a rádióamatőr képzés keretében lehetőség van iskolai- vagy klubeszközökkel dolgozni,
akkor végezzük el egyszer a következő kísérletet.
Építsük meg a 4. ábrán látható rezgőkört a következő alkatrészekkel: L=100mH és C=10nF.
Kapcsoljunk vele a sorba egy váltakozó áram mérésére alkalmas árammérőt, lehetőleg alacsony belső ellenállásút.
Változtassuk a frekvenciát kb. 100 Hz és 10 kHz között, és mérjük meg az áramot.
Figyeljünk arra, hogy a generátor feszültsége lehetőleg változatlanul maradjon.
Ha nincs lehetőségük a mérésre, a következő táblázatból olvashatjuk le a tipikus mérési értékeket. Megjegyzés: a ténylegesen mért áram lehet kisebb és nagyobb is. Ez a tekercs ellenállásától és a generátor belső ellenállásától függ.
Állandó, 2,5 V-os generátorfeszültég mellett a következő értékek mérhetők:
| f | 1 | 2 | 3 | 4 | 4,7 | 5 | 5,3 | 6 | 7 | 10 | kHz |
| I | 3 | 5 | 8 | 16 | 70 | 100 | 70 | 20 | 12 | 5 | mA |
| Z | 125 | W |
Feladat
Rajzoljuk be az előbb mért áramértékeket a 5. ábrán bal oldalán látható diagramba.
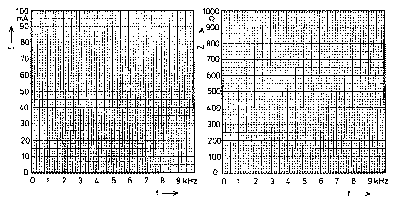
5. ábra: Az áram és a látszólagos ellenállás a frekvencia függvényében
Ha váltóáram esetén az feszültséget az átfolyó árammal elosztjuk, akkor - hasonlóan, mint az Ohm törvénynél - egy ohmban mért ellenállásértéket kapunk. Ezt az értéket ebben az esetben látszólagos ellenállásnak nevezzük és Z-vel jelöljük. 6 kHz frekvenciánál és U=2,5 V-nál például 20 mA-t mértünk. Ebből a látszólagos ellenállás:
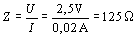
Feladat
Számoljuk ki a mért értékekből (vagy a fenti táblázatból) a látszólagos ellenállást a megadott frekvenciák esetén. Írjuk be az eredményeket a táblázatba, és rajzoljuk be az 5. ábra jobb oldalán látható diagramba.
Ha jól számoltunk és rajzoltunk, akkor egy olyan görbét kapunk, amelyen f=5 kHz-nél van az árammaximum és a látszólagos ellenállás minimuma.
Az ilyen görbét, ahol az áram, a feszültség, vagy a látszólagos ellenállást vizsgáljuk a rezgőkör frekvenciájának függvényében rezonanciagörbéknek nevezzük. A látszólagos ellenállást rezonanciafrekvenciánál rezonanciaellenállásnak nevezzük. Ez soros rezgőkör esetén kis értékű, a példánkban 25 ohm. (Lásd a TD509-es tesztkérdést!)
Ezek az alacsony frekvencián elvégzett számolások magas frekvencián is érvényesek. Ehhez azonban még hozzájönnek az ohmos veszteségeken kívül (a tekercs huzaljának ellenállása) a mag anyagából származó veszteségek valamint a vezeték skineffekt folytán lecsökkenő vezetőképessége miatti veszteség. Megjegyzés: skineffektus (bőreffektus) lényege, hogy a váltakozó áram által átjárt vezetőkben az áramsűrűség a vezető belsejében kisebb, mint a vezető felületén.
Jegyezzük meg: A soros rezgõkörnek kicsi a rezonanciaellenállása. Körülbelül akkora, mint a tekercs ohmos ellenállása.
A 6. ábrán a soros rezgõkör rádióamatõr technikában való egyik tipikus felhasználását láthatjuk.
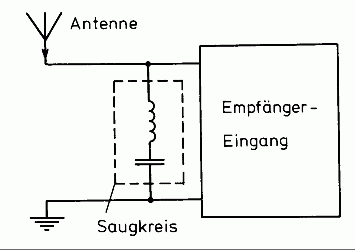
6. ábra: Soros rezgõkör mint szívókör
Egy soros rezgõkör egy bizonyos frekvencián (a rezonanciafrekvencián) gyakorlatilag rövidzárként mûködik. Emiatt a tulajdonsága miatt használják vevõkben a nemkivánatos bementi jelek kiszûrésére. Lásd TD513-as tesztkérdés.
A párhuzamos rezgõkör
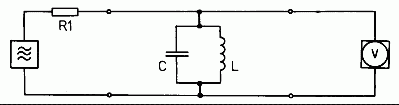
7. ábra: Kísérleti elrendezés a párhuzamos rezgõkör rezonanciagörbéjének méréséhez
Kísérlet:
Kapcsoljuk a két áramköri elemet (L-t és C-t), amit a soros rezgõkörnél használunk
a 7. kép alapján párhuzamosan.
Az áram állandó szinten tartása érdekében növeljük meg a generátor belsõ ellenállását egy
1 megaohmos ellenállás sorbakapcsolásával. Ezután mérjük meg a rezgõkörre esõ feszültséget a frekvencia függvényében. A feszültségméréshez elektronikus váltófeszültség-mérőt, de akár
oszcilloszkópot is használhatunk.
A következõ táblázatban lévõ eredményekhez hasonlókat kaptuk?
| f | 1 | 2 | 3 | 4 | 4,7 | 5 | 5,3 | 6 | 7 | 10 | kHz |
| U | 0,02 | 0,04 | 0,06 | 0,1 | 0,7 | 1 | 0,7 | 0,15 | 0,1 | 0,05 | V |
| Z | 20 | 333 | kΩ |
Feladat:
Számítsuk ki miden mérési ponthoz a látszólagos ellenállást és írjuk be a fenti táblázatba.
Két mezőt márkitöltöttünk.
Feladat:
Rajzoljuk be a 8. ábrába a mért feszültés és a látszólagos ellenállás görbéjét.

5. ábra: Párhuzamos rezgőkörön eső feszültség (balra) és a látszólagos ellenállás (jobbra) a frekvencia függvényében.
A soros rezgõkörnél látott görbékhez hasonlókat kell kapnunk, azzal különbséggel, hogy itt mindkét esetben maximum van.
Jegyezzük meg:
A párhuzamos rezgõkör látszólagos ellenállása a rezonanciafrekvencián a legnagyobb.
Ha a rezgõkört egy nagy belsõ ellenállású generátorral gerjesztjük, akkor ezen a frekvencián éri el a feszültség is a maximumát. E tulajdonsága miatt használják a párhuzamos rezgõkört az adók és vevõk nagyfrekvenciás erõsítõiben. Az erõsítendõ feszültség a rezonanciafrekvencián éri el a maximumát. A párhuzamos rezgõkör egy másik felhasználása a zárókör. Ha egy párhuzamos rezgõkört sorbakapcsolunk egy vevõ bemenetével, akkor az kiszûri a rezonanciafrekvencia környékén levõ frekvenciákat, mert a párhuzamos rezgõkör ebben a frekvenciatartományban egy nagy értékű ellenállásként viselkedik. Lásd TD511-es tesztkérdést!
Öszzefoglalás:
A párhuzamos rezgõkör látszólagos ellenállása a reznonciafrekvencián a legnagyobb. A soros rezgõköré ugyanakkor a legkisebb (9. ábra).
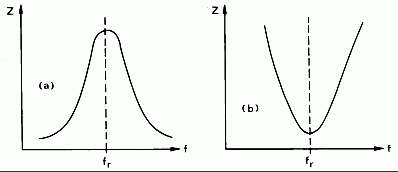
9. ábra: Párhuzamos (a) és soros (b) rezgõkör látszólagos ellenállása.
A sávszélesség
Egy nagyfrekvenciás erõsítõ, amelynek munkaellenálása egy rezgõkör, nemcsak egyetlen frekvenciát erõsít, hanem egy frekvenciatartományt. Azt a tartományt nevezzük sávszélességnek (kép 10), amelyen belül a feszültség, vagy a látszólagos ellenállás a maximális értékéneek 70%-át megahaldja.
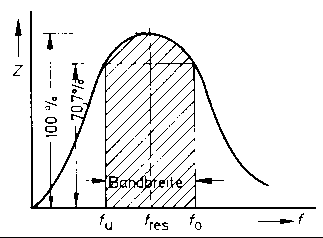
10. ábra: A párhuzamos rezgõkör sávszélessége
Alul- és felüláteresztő szűrők
Az eddig vizsgált kapcsolásokhoz további induktivitás és kondenzátor hozzákapcsolásával alul- és felüláteresztő szűrőkhöt jutunk.

11. ábra: Az aluláteresztõ szûrõ (balra) és a hozzátartozó átviteli karakterisztika (jobbra).
Ha a jel útjával sorosan egy tekercset, és mögé egy kondenzátort a jel útjával párhuzamosan kapcsolunk, akkor egy aluláteresztõ szûrõt kapunk (11. äbra). Az aluláteresztõ hatás a következõképpen áll elõ: ha a frekvencia viszonlag alacsony, akkor a tekercs kis induktív ellenállásként viselkedik, a kondenzátor pedig nagy kapacitív ellenállásként. Egy feszültségosztó áll elõ, ahol egy kicsi ellenállás van sorbakapcsolva egy nagy ellenállással, és a kimeti feszültséget a nagy ellenállásról vesszük le. Csak kevés feszültség esik a kicsi ellenálláson, a kimeneti feszültség majdnem akkora, mint a bemeneti feszültség (lásd a 11. ábra jobb oldalát).
A frekvencia növelésével az induktív ellenállás növekszik és a kapacitív pedig csökken. Egyre több feszültség esik az induktivitáson. A magas frekvenciák tehát nem jutnak jól át, másképp mondva: a kapcsolás az alacsony frekvenciákat jól átereszti - azaz aluláteresztõ szûrõ. Azt a frekvenciát, ahol a kimeneti feszültség még 70%-a a bemeneti feszültségnek, határfrekvenciának nevezzük.
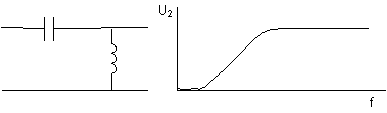
12. ábra: A felüláteresztõ szûrõ (balra) és a hozzátartozó frekvenciakarakterisztika (jobbra).
A 12. és a 11. ábra kapcsolása között csak annyi a különbség, hogy a kondenzátort és az induktivitást megcseréltük. Ha a frekvencia alacsony, akkor a sorosan kapcsolt kondenzátor nagy ellenállásként viselkedik, és az induktivitás pedig kicsiként. Ezért csak kis feszültség jut a kimenetre. Csak nagyfrekvenciánál engedi át a kondenzátor az áramot, és ekkor a tekercs sem viselkedik már rövidzárként - ez tehát egy nagyfrekvenciás szûrõ.
Ezeket a kapcsolásokat elég gyakran alkalmazzák a rádióamatõr technikában. Például egy adóállomás mellett fellépő rádió- vagy televízióvételi zavarok esetén használható egy olyan szűrő, amely a rövidhullámú jeleket nem engedi át, az URH és TV jeleket viszont igen.
Tesztkérdések
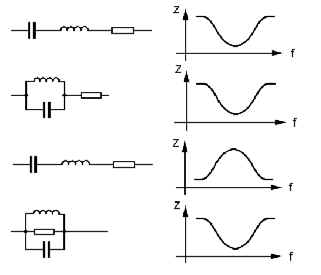
TD509*) Melyik rezgőkör illik a mellette lévő látszólagos ellenállás -- frekvencia függvényhez?
TD510 Mit ábrázol a következő kapcsolás?

- a) aluláteresztő szűrő
- b) sáváteresztő szűrő
- c) sávzáró szűrő
- d) felüláteresztő szűrő
TD511 Mit ábrázol a következő kapcsolás?
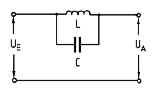
- a) felüláteresztő szűrő
- b) sávzáró szűrő
- c) szívókör
- d) aluláteresztő szűrő
TD512 Mit ábrázol a következő kapcsolás?
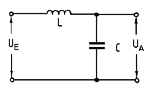
- a) felüláteresztő szűrő
- b) aluláteresztő szűrő
- c) szívókör
- d) sávzáró szűrő
TD513 Mit ábrázol a következő kapcsolás?
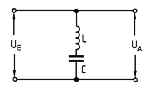
- a) sávzáró szűrő
- b) felüláteresztő szűrő
- c) szívókör
- d) aluláteresztő szűrő
TD514 A következő állítások közül melyik igaz a felüláteresztő szűrőre?
- a) A határfrekvencia fölötti frekvenciákat engedi át
- b) A határfrekvencia alatti frekvenciákat erősíti
- c) A határfrekvencia feletti frekvenciákat csillapítja
- d) A határfrekvencia alatti frekvenciákat csillapítatlanul átengedi
 © http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:34
© http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:34
Eredeti mű: © Eckart Moltrecht DJ4UF, http://www.amateurfunkpruefung.de