Kondenzátor
Mi is a kondenzátor?
Az eddigi leckékben megismerkedtünk az ellenállással, mint az elektronika egyik fontos építőelemével, és alkalmazási módjaival. Ebben a leckében megismerhetjük, az elektronikai készülékek, az adó és vevő készülékek másik hasonlóan fontos szerepet játszó alkatrészét, a kondenzátort.
A kondenzátor két, egymás mellett lévő, szigetelőanyaggal elválasztott fémlemezből (vezetőből) áll. (lásd 1. ábra) A két fémlemezt fegyverzetnek, a szigetelőt dielektrikumnak nevezik.
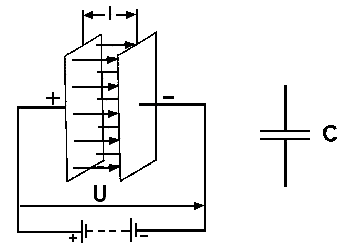
1. ábra: A kondenzátor felépítése és jelölése
Az elektromos térerő
Abban az esetben, ha a kondenzátor két fémlemezére egyenfeszültséget kapcsolunk, közöttük elektromos mező keletkezik. Az elektromos mező nagysága függ a feszültség mértékétől, és a fegyverzet egymástól való távolságától. Minél nagyobb a feszültség (U), illetve minél kisebb a fegyverzetek egymástól való távolsága (l), annál nagyobb elektromos mező alakul ki.
Elektromos térerő:
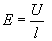
Figyelem! A képlet nem azonos az U osztva I-vel, mint pl. az ellenállásoknál, hanem U osztva l-el (kis "L").
A térerő egy bizonyos értéke felett a dielektrikum vezetővé válik, ami annyit jelent, hogy a kondenzátor "átüt". Az elektroncsöves adó végfokozatok igen nagy feszültségekkel működnek, ezért ott olyan kondenzátorokat alkalmaznak, melyeknek fegyverzetei között relatív nagy távolság van, elkerülve ezzel a kondenzátor átütését.
Példa
Egy kondenzátor fegyverzetére 250 V feszültséget kapcsolunk, ahol a fegyverzet egymástól való távolsága 1 mm. Mekkora az elektromos térerő?
Megoldás
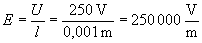
A kapacitás
A fegyverzetek között lévő dielektrikum elektromosan szigetelő. A szigetelők csak kevés szabad elektront tartalmaznak.
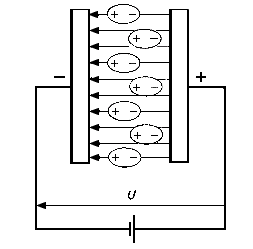
A szigetelők egy része olyan molekulákból áll, amelyek külső elektromos tér hiányában nem polárosak, külső elektromos tér hatására viszont polarizálódnak. A szigetelők másik típusában a molekulák már szerkezetüknél fogva dipólusosak, de külső elektromos tér nélkül teljesen rendszertelenül helyezkednek el. Elektromos tér hatására viszont dipólláncot alkotva igyekeznek beállni a tér irányába. A jelenséget dielektromos polarizációnak hívjuk. (2. ábra) Elektromos térben a szigetelő egyik oldala pozitívvá, a másik negatívvá válik, hasonlóan a vezetőknél tapasztalt elektromos megosztáshoz.
A lényeges különbség a kettő között az, hogy míg a vezetők esetében jelentős töltésmozgás van, addig itt nincs töltésáramlás, csak a molekulaláncok végein jelentkező töltések mutatkoznak meg. A külső elektromos tér hatására a szigetelő molekuláiban a töltések szétválnak, a polarizálódott részecskék pedig beállnak a tér irányába.
A kondenzátor pozitív töltésű lemezéről induló erővonalak egy része a szigetelő szomszédos dipólusos részecskéin végződik. Hasonló dolog történik a negatív töltésű fegyverzeten is, csak itt az erővonalak a szomszédos részecskékről indulnak és a negatív lemezen végződnek. Ezáltal jóval kevesebb erővonal jut át egyik lemezről a másikra.
Az elektromos teret megszüntetve, a részecskék polarizációja miatt a töltések a fegyverzeteken megmaradnak.
A kondenzátor lemezein tehát elektromos töltések tárolhatók. A tárolóképességet kapacitásnak nevezzük, jele: "C". Minél nagyobb a kondenzátor kapacitása, annál több elektromos töltést "Q" képes tárolni.
Q = C × U
A kapacitás "C" nagysága függ a fegyverzetek felületeinek "A" nagyságától, a köztük lévő távolságtól "l", valamint a dielektrikum anyagától. A dielektrikum anyagától függ, hogy benne mekkora dipóllánc képes kialakulni, ezáltal befolyásolva a kondenzátor tároló kapacitását. Az anyagnak a villamos teret befolyásoló hatására jellemző mennyiséget dielektromos állandónak, (permittivitásnak) nevezik, jele a görög ε, (epszilon). A villamos permittivitás a tér valamely pontjában a vákuum permittivitásának és a teret az adott pontban kitöltő anyag vákuuméhoz viszonyított, relatív permittivitásának szorzata, ahol ε0 a vákuum permittivitása, illetve dielektromos térállandója, εr dimenzió nélküli számérték, az anyag relatív permittivitása, vagy relatív dielektromos térállandója. Az anyagra jellemző permittivitás tehát a villamos tér anyagtól független, illetve a teret kitöltő anyagtól függő jellemzője közötti kapcsolatot határozza meg.
ε = ε0 × εr
A levegő εr értéke: kb. 1 (1,00059).
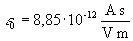
A kapacitás mértékegysége a farad, jele: F.
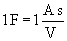
Az 1 F nagyon nagy egység, a gyakorlatban a kisebb egységeit használjuk.
1 mikrofarad = 1 µF = 10-6 F = 1000 nF
1 nanofarad = 1 nF = 10-9 F = 1000 pF
1 pikofarad = 1 pF = 10-12 F
Egy kondenzátor kapacitását a geometriai méreteiből is ki tudjuk számolni.
A képletről a következőket olvashatjuk le. Minél nagyobb a felület "A", annál nagyobb a kapacitás "C". A távolság "d" növekedésével, pedig csökken a kapacitás. Az ε a fegyverzet közötti anyagot (dielektrikumot) jelöli. ε0 a vákuum permittivitása, εr az anyag relatív permittivitása.
Vizsgakérdések
TC508 Mely tényezőktől nem függ egy lapkondenzátor kapacitása?
a) feszültség
b) fegyverzetek távolsága
c) fegyverzetek felülete
d) dielektrikum
Tipp: Nézzük meg a fenti képletet, és keressük meg melyik nem szerepel benne? Feszültség (U), fegyverzetek távolsága (d), fegyverzetek felülete (A) és a dielektrikum ε.
TC509 Melyik kifejezés hamis?
a) Nagyobb dielektrikum permittivitás esetén nagyobb a kapacitás
b) Több lemez esetén nagyobb a kapacitás
c) Nagyobb felület esetén nagyobb a kapacitás
d) Nagyobb lemeztávolság esetén nagyobb a kapacitás
Kondenzátorok párhuzamos kapcsolása
Az ellenállásokhoz hasonlóan, a kondenzátorok esetében is létezik soros, párhuzamos és vegyes kapcsolás.
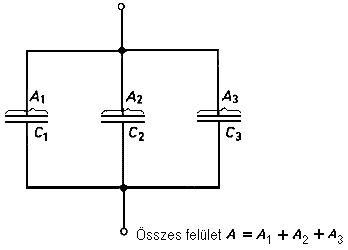
3. ábra: Kondenzátorok párhuzamos kapcsolása
Kondenzátorok párhuzamos kapcsolása esetén, megnő a hatásos felület a lemezekkel szemben, nagyobb arányú felület esetén pedig nő a kapacitás. Megjegyzés:
Kondenzátorok párhuzamos kapcsolása esetén az egységnyi kapacitásértékek összeadódnak.
Vizsgakérdések TD506
Három darab kondenzátort kapcsolunk párhuzamosan. Az értékek: C1 = 0,1 µF, C2 = 150 nF és C3 = 50000 pF.
Mekkora az együttes kapacitás?
Megoldás
A kapacitásértékeket váltsuk át egy egységes értékre, például nanofarad-ra (nF).
1000 pF = 1 nF, 1000 nF = 1 µF. Az átváltott értékek: C1 = 100 nF, C2 = 150 nF és C3 = 50 nF
C = 100 nF + 150 nF + 50 nF = 300 nF = 0,3 µF.
A 0,3 µF mint megoldás, megtalálható a feladat lehetséges válaszaiban. (lásd vizsgakérdések)
Kondenzátorok párhuzamos kapcsolásainak számításainál ugyanúgy számolunk, mint az ellenállások soros kapcsolása esetén.
Kondenzátorok soros kapcsolása

4. ábra: Kondenzátorok soros kapcsolása
Több kondenzátor sorba kapcsolása (4. ábra) a fegyverzet távolságának növelését jelenti. A soros kapcsolás együttes kapacitása mindíg kisebb, mint a kapcsolásban lévő legkisebb kapacitás értéke.
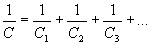
Kondenzátorok soros kapcsolásainak számításainál ugyanúgy számolunk, mint az ellenállások párhuzamos kapcsolása esetén.
Vizsgakérdések TD507
Mekkora az együttes kapacitás értéke soros kapcsolás esetén? Értékek: 0,1 µF, 150 nF és 50000 pF
Megoldás A kapacitásértékeket váltsuk át egy egységes értékre, mint az TD506-os feladat esetében. C1 = 100 nF, C2 = 150 nF és C3 = 50 nF Értékek behelyettesítése a képletbe:
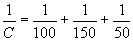
Számológéppel a következőképpen számolhatjuk ki a kívánt eredményt. Számoljunk együtt!
Írjuk be: 100 - 1/x-gombot megnyomni - plusz gombot megnyomni - írjuk be 150 - 1/x-gombot megnyomni - plusz gombot megnyomni - írjuk be 50 - 1/x-gombot megnyomni - egyenlő (=) gombot megnyomni - és még egyszer 1/x-gombot megnyomni. A kijelzőn megjelenő érték: 27,272727.
Tehát 27,3 nF vagy 0,027 µF. A 0,027 µF mint megoldás, megtalálható a feladat lehetséges válaszaiban. (lásd vizsgakérdések)
Két kondenzátor esetén a számítást a következő képlettel is elvégezhetjük:
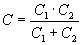
Vizsgakérdések
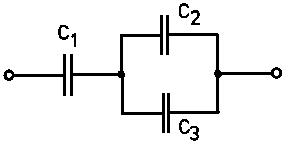
Számítsuk ki a vegyes kapcsolású kondenzátorok eredő kapacitását C1 = 0,01 µF, C2 = 5 nF, C3 = 5000 pF
Megoldás
A kapacitásértékeket váltsuk át egy egységes értékre, például nanofarad-ra (nF). 1000 pF = 1 nF, 1000 nF = 1 µF.
A kapott értékek: C1 = 10 nF, C2 = 5 nF és C3 = 5 nF
Számítsuk ki a párhuzamosan kapcsolt C2 és C3 értékét.
C2/3 = C2 + C3 = 5 nF + 5 nF = 10 nF
majd számoljuk ki a C1 és C2/3 értékét.
A kondenzátor egyenáramú áramkörben
Amennyiben a kondenzátorra egyenfeszültséget kapcsolunk, akkor az feltöltődik. Tegyünk egy próbát! 6. ábra.
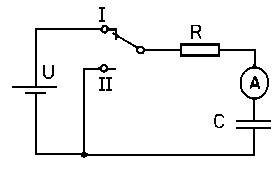
6. ábra: A kondenzátor feltöltése (I-es kapcsolóállás) és kisütés (II)
A töltés kezdetén egy rövid időre az ampermérő nagy áramfelvételt mutat, ami az idő múlásával folyamatosan csökken. (7. ábra).
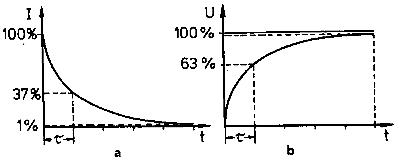
7. ábra: Áram (a) és feszültség (b) értékek a kondenzátor töltése közben
A töltési időt az időállandó-val jelöljük, melynek jele: τ (ejtsd: tau). Ez idő alatt a feszültség eléri a töltési feszültség 63%-át, az áram, pedig a kezdeti érték 37%-ára csökken.
Jegyezzük meg a töltés közbeni feszültségérték változását. A töltés kezdetén az érték nulláról indul, hirtelen meredeken, majd később lassabban nő. (lásd TB524-es feladat!)
Kisütéskor hasonlóképpen játszódik a folyamat. (6. ábra II-es kapcsolás).
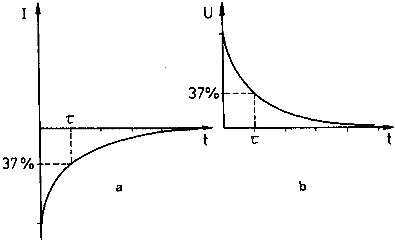
8. ábra áram (a) és feszültség (b) értékek a kondenzátor kisütésénél
Egy U feszültségre teljesen feltöltött kondenzátor az R ellenálláson keresztül sül ki.
Az időállandó alatt az áram (-I) a kezdeti érték 37%-ára, a feszültség értéke pedig nullára csökken.
A kondenzátor váltakozó áramú ellenállása
Folyamatosan ismétlődő töltések és kisütések esetén a következő feszültség és áramerősség változások figyelhetők meg (9. ábra).
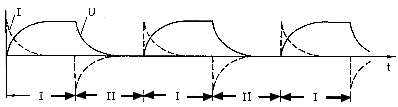
9. ábra: Kondenzátor ismétlődő töltése (I) és kisütése (II)
Abban az esetben, ha a kondenzátorra váltakozó feszültséget kapcsolunk, ismétlődő töltést és kisütést figyelhetünk meg. Az áramkörbe kapcsolt ampermérőn a töltési és kisütési áram összegét olvashatjuk le. (10. ábra).
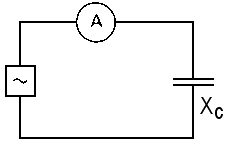
10. ábra: Kondenzátor váltakozó feszültségű áramkörben
Kondenzátorok esetében is, mint az ellenállásoknál az Ohm-törvényben ismert képletet alkalmazhatjuk. A kondenzátor váltakozó áramú ellenállása: XC.
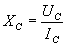
Relatív magas frekvencia esetén, váltakozó áramú áramkörökben a feszültség és áramerősség pontos értékei csak nehezen mérhetők. A kondenzátor váltakozó áramú ellenállásának méréséhez ezért szükségünk van egy képletre, amivel az XC értéke a kapacitás és a frekvencia értékeivel kiszámítható.
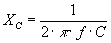
A képlet segítségével a kondenzátor váltakozó áramú ellenállása a kapacitás és a frekvencia (f) értékek ismeretével kiszámítható. A törtvonal alatti π (ejtsd: "pi") értéke: 3,14.
TC504-es feladat Számítsuk ki egy 50 pF kapacitású kondenzátor váltakozó áramú ellenállását, 145 MHz esetében!
Megoldás:
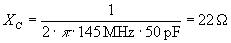
Utasítás: Számológéppel való számolásnál a (piko) értékénél -12, a (mega) értékénél +6 exponenst kell megadni. Számoljunk együtt! 2-es számot írjuk be - szorzás gombot (×) nyomjuk meg - π-gombot (pi) nyomjuk meg - szorzás gombot (×) nyomjuk meg - 145-ös számot írjuk be - EXP-gombot nyomjuk meg és adjunk meg 6-ot - szorzás gombot (×) nyomjuk meg - 50-es számot írjuk be - EXP-gombot nyomjuk meg és a +/- előjelváltóval váltsunk mínusz előjelre, majd adjunk meg 12-őt - egyenlőség gombot (=) nyomjuk meg, majd végezetül az 1/×-gombot nyomjuk meg - készen is vagyunk. A kijelzőn megjelent eredmény 21,952406, kerekítve 22 Ohm.
Feladat: oldjuk meg a TC505, TC506 és a TC507 feladatokat!
Elektrolit kondenzátorok polaritás függőek, ami azt jelenti, hogy beépítéskor ügyelnünk kell a helyes polaritásra. (+/-) (TC524-es vizsgakérdés).
Az TC533 - TC535 vizsgakérdések megválaszolásánál tudnunk kell még azt, hogy a kondenzátorokon milyen formában jelölik az értékeket. Például egy kondenzátor esetében az 5p6 jelölés 5,6 pF vagy m33 jelölés 0,33 mF, tehát 330 µF jelent. A nulla nincs jelölve.
Vizsgakérdések
TC504 Mekkora egy 50 pF kapacitású kondenzátor váltakozó áramú ellenállása 145 MHz-en?
a) 0,045 Ω
b) 22 Ω
c) 69 Ω
d) 18,2 kΩ
TC505 Mekkora egy 100 pF kapacitású kondenzátor váltakozó áramú ellenállása 435 MHz-en?
a) 0,27 Ω
b) 3,7 Ω
c) 11,5 Ω
d) 27,3 kΩ
TC506 Mekkora a kapacitív ellenállása egy 10 pF-os kondenzátornak 100 MHz-en?
a) 31,8 Ω
b) 159 Ω
c) 318 Ω
d) 1,59 kΩ
TC507 Mekkora a kapacitív ellenállása egy 100 pF-os kondenzátornak 100 MHz-en?
a) 3,2 Ω
b) 15,9 Ω
c) 31,8 Ω
d) 159 Ω
TC508 Mely tényezőktől nem függ egy lapkondenzátor kapacitása?
a) feszültség
b) fegyverzetek távolsága
c) fegyverzetek felülete
d) dielektrikum
TC509 Melyik kifejezés hamis?
a) Nagyobb dielektrikum permittivitás esetén nagyobb a kapacitás
b) Több lemez esetén nagyobb a kapacitás
c) Nagyobb felület esetén nagyobb a kapacitás
d) Nagyobb lemeztávolság esetén nagyobb a kapacitás
TB524 A diagrammok közül melyik jelöli a kondenzátor "R" ellenálláson keresztüli egyenfeszültségű "U" feltöltését?
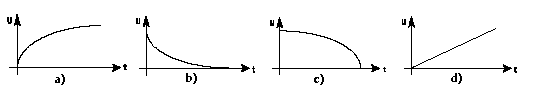
TC524 Melyik alkatrész alkalmazásánál nem kell ügyelnünk a polaritás helyességére?
a) akkumulátor
b) elektrolit-kondenzátor
c) ellenállás
d) dióda
TC533 Egy kondenzátoron a következő jelölés olvasható: " m33 ". Mekkora kapacitást jelent a felirat?
a) 3,3 µF
b) 33 µF
c) 330 µF
d) 33000 µF
TC534 Egy kondenzátoron a következő jelölés olvasható: " n47 ". Mekkora kapacitást jelent a felirat?
a) 4,7 pF
b) 47 pF
c) 470 pF
d) 47000 pF
TC535 Egy kondenzátoron a következő jelölés olvasható: " 8p2 ". Mekkora kapacitást jelent a felirat?
a) 0,82 pF
b) 8,2 pF
c) 82 pF
d) 820 pF
TD505 Három darab kondenzátort sorba kapcsoltunk. Mekkora az eredő kapacitás, ha az értékek a következők: C1 = 0,06 nF, C2 = 40 pF és C3 = 20 pF?
a) 8,1 pF
b) 10,9 pF
c) 30 pF
d) 0,12 nF
TD506 Három darab kondenzátort párhuzamosan kapcsoltunk. Mekkora az eredő kapacitás, ha az értékek a következők: 0,1 µF, 150 nF és 50000 pF?
a) 2,73 nF
b) 0,027 µF
c) 0,255 µF
d) 0,3 µF
TD507 Három darab kondenzátort sorba kapcsoltunk. Mekkora az eredő kapacitás, ha az értékek a következők: 0,1 µF, 150 nF és 50000 pF?
a) 2,73 nF
b) 0,027 µF
c) 0,255 µF
d) 0,3 µF
TD508 Mekkora az eredő kapacitás?

a) 0,015 nF
b) 5 nF
c) 7,5 nF
d) 12,5 nF
A helyes megoldások részletei a következő linken találhatók: Függelék
Tesztfeladatok
A következő táblázatban a feladat számára kattintva megtekinthetők a megoldások.
| TC504 | TC505 | TC506 | TC507 | TC508 | TC509 | TB524 | TC524 |
| TC533 | TC534 | TC535 | TD505 | TD506 | TD507 | TD508 |
A helyes válaszok száma több mint 12? Jó!
 © http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:33
© http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:33
Eredeti mű: © Eckart Moltrecht DJ4UF, http://www.amateurfunkpruefung.de