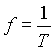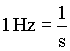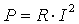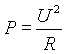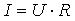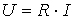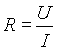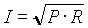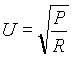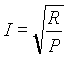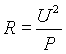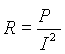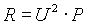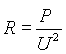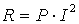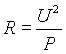Teljesítmény, munka

Ismétlés

Ez a fejezet nagyon fontos elektrotechnikai elméleti alapokat tartalmaz, amelyek nélkül nehéz lenne a továbbiakat megérteni. Az elsajátításhoz segítséget nyújt a sok gyakorló feladat, amelyek az Ohm-törvényhez, teljesítményhez, munkához kapcsolódnak.

Időközben megismerkedtünk a feszültség és a villamos áramerősség fogalmával, valamint a váltakozó-áramú mennyiségekkel, mint például a frekvencia, hullámhossz stb.

Mennyiség neve	Jelölés	Mértékegység	Mértékegység jele
feszültség	U	volt	V
áramerősség	I	amper	A
periódusidő	t	másodperc	s
frekvencia	f	hertz	Hz
hullámhossz	l	méter	m

A megismert mennyiségek között már felírható a következő kapcsolat:

Mennyiségekkel	Mértékegységekkel

A következő oldalakon a feszültség és áram kapcsolatára visszavezethető fogalmakról lesz szó.

Az Ohm-törvény

A következő ábrán egy kísérlet látható. Ha növeljük a forrásunk feszültségét, akkor az áramkörbe kötött izzó fényesebben világít. Ez azt mutatja, hogy akkor nagyobb áram folyik az áramkörben.

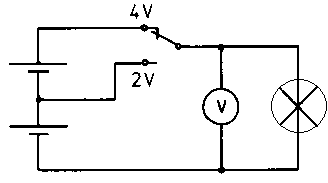
Végtelen nagy áram nem folyhat a körben. Az izzóban lévő vezető szál ellenállása korlátozza a kialakuló áram nagyságát. Az ellenállást befolyásolja a vezetőanyagban lévő szabad elektronok száma, valamint az anyag rácsszerkezete. Ezekről a további fejezetekben lesz szó részletesen.

Az izzólámpa ellenállását és minden más ellenállást a következő szimbólummal ábrázoljuk:

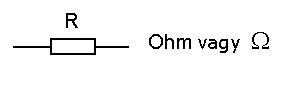
Az R betű az ellenállás mennyiségének jele (az angol resistor szóból származik), a mértékegysége pedig ohm, jele: Ω.

Definíció: Ha a fogyasztóra kapcsolt 1 V feszültség hatására 1 A áram folyik, akkor a fogyasztó ellenállása 1 ohm.

A mértékegységet 1970-ben határozták meg pontosan: Az elektromos ellenállás származtatott SI egysége az ohm (1 ohm az ellenállása annak a homogén szerkezetű fém vezetőnek, amelynek két pontja között, állandó hőmérsékleti viszonyok között, 1V feszültség hatására, állandó erősségű, 1 A nagyságú áram folyik.)

Tehát bármelyik két mennyiségből meghatározható a harmadik.

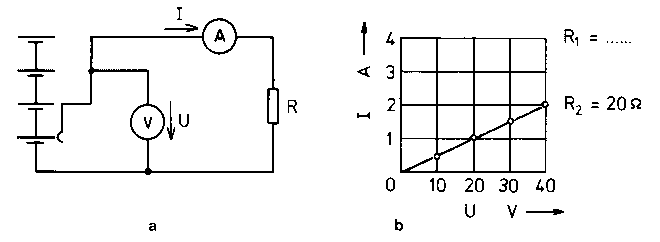
A mérési összeállítás (a) és a mérhető karakterisztika (b)

Első kísérlet:

Állandó ellenálláson (10 ohm) változtatjuk a feszültséget és mérjük az áramot.

U (V)	10	20	30	40
I (A)	1	2	3	4

A mért értékeket egy U-I diagramon ábrázolva egy egyenes pontjait kapjuk. Ha az egyenest megrajzoljuk, láthatjuk, hogy az origón halad át, tehát 0 feszültség esetén nem folyik áram. Ha megismételjük a mérést egy másik (pl 20 ohm-os) ellenállással, akkor is az látható, hogy kétszer akkora feszültség hatására kétszer akkora áram folyik. Ezt úgy is mondhatjuk, hogy feszültség és az áramerősség egyenesen arányos. Írásban: U~I.

Második kísérlet:

Az áramot állandó értéken tartva (2 A) változtatjuk az ellenállást. Mérjük az áram fenntartásához szükséges feszültséget.

R (ohm)	5	10	20
U (V)	10	20	40

Látható, hogy az ellenállás és a feszültség között is egyenes arányosság van: R~U.

Mindkét tapasztalt kapcsolatot az Ohm-törvény írja le:

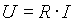
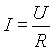
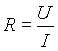
Az Ohm-törvény segítségével megismerhettük a kapcsolatot két alap menyiség, a feszültésg és az áramerősség között. A kapcsolat érvényes egyenáram (DC) és váltakozó mennyiségek (AC) esetén is.

Első példa:

Mekkora feszültség szükséges egy jelfogó működtetéséhez, ha 50 ohm-os tekercsén 120 mA-nek kell átfolyni ahhoz, hogy az érintkezők meghúzzanak?

Adott: R = 50 ohm, I = 120 mA = 0,12 A
U = R*I = 50*0,12 = 6
Tehát 6 V szükséges a működtetéshez.

Második példa:

Egy elektronikus eszközre 24 V feszültséget kapcsolva 15 mA áram indul meg a körben. Mekkora az eszköz ellenállása?

Adott: I = 15mA = 0,015 A; U = 24V
R = U/I = 24/0,015 = 1600
Tehát az eszköz ellenállása 1600 ohm, azaz 1,6 kohm.

Érdemes megjegyezni (villamos szakember számára hasznos lehet):

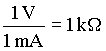
vagy

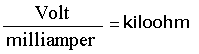
Ezek segítségével a 2. példa gyorsan számítható:

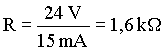
Első gyakorlat:

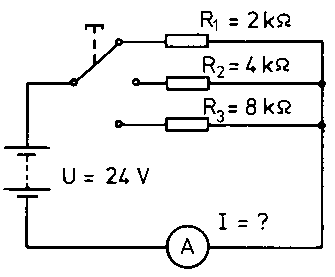
Egy háromállású kapcsolóval három különböző értékű ellenállást kapcsolhatunk az áramkörbe. Mekkora áramerősség mérhető az egyes esetekben? Megoldás (egészítsük ki a táblázatot):

R (kohm)	2	4	8
I (mA)	...	...	...

A megoldás helyessége könnyen ellenőrizhető, hiszen az ellenállás kétszeresére változtatásával az áramerősségnek mindig felére kell csökkennie.

Második gyakorlat:

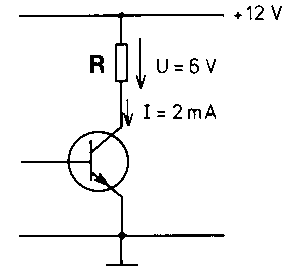
Az ábrán látható tranzisztoros kapcsolásban lévő munkaellenállás értékét kell meghatározni. A kapcsolás tápfeszültsége 12 V. Azt szeretnénk, hogy a tápfeszültség fele legyen a munkaellenálláson. A tranzisztor NF erősítőként alkalmazására 2 mA kollektoráramot ír elő a gyártó.

Mekkora értékű kollektor ellenállást válasszunk?

A) 6 kohm B) 3 kohm C) 333 ohm D) 166 ohm

A villamos teljesítmény

A szükséges teljesítmény függ a fogyasztó ellenállásának nagyságától. Mekkora a maximális teljesítmény az előző tranzisztoros kapcsolásban szereplő ellenálláson? A kérdés megválaszolása a következő sorok után már egyszerűbb lesz.

Ha egy ellenálláson áram folyik, akkor az ellenálláson hő termelődik (vasaló, izzó). Ez a teljesítmény növekszik, ha akár a feszültség, akár az áramerősség növekszik a fogyasztón. Az elektromos teljesítmény jele: P (az angol power szóból), az áram és feszültség szorzataként számítható.

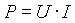
A teljesítmény mértékegysége a watt [W], V*A. A fogysztón lévő teljesítmény 1 W, ha 1 V feszültség hatására 1 A áram folyik rajta keresztül.

1 W = 1 V * 1 A

Gyakran használjuk a következő prefixekkel teljesítmény mértékegységét:

1 megawatt	MW	10^6 W
1 kilowatt	kW	10^3 W
1 milliwatt	mW	10^-3 W
1 mikrowatt	μW	10^-6 W

A P = U*I kiszámítási mód alapvetően csak egyenáram esetén igaz minden esetben. Váltakozó mennyiségek esetén csak akkor használható, ha a feszültség és áram között nincs fáziseltérés, azaz csak tisztán ohmos terhelés van az áramkörben. (Bővebben lásd. a 3. fejezetben)

Részletesebben nem foglalkozunk most ezzel a témakörrel, mert ennyi elegendő a rádióamatőr vizsgához.

Példa:

Mekkora a teljesítmény a második gyakorlatban szereplő ellenálláson, ha a 6 V feszültség hatására 2 mA áram folyik át rajta?

Adott: U = 6 V; I = 2 mA

Keressük: P

Megoldás: P = U*I P = 6 V * 2 mA = 12 mW

Tehát mindössze 12 mW (hő)teljesítmény adódik az ellenálláson (Joule-hő).

Harmadik gyakorlat:

Egy mobil adó-vevő adáskor 100 W teljesítményt vesz fel az autó 12 V-os rendszeréből.
Mekkora a felvett áramerősség?

A) 1200 A B) 16,6 A C) 8,33 A D) 0,12 A

Ha nincs megadva a feszültség és az áram, hanem csak a feszültség-ellenállás vagy a áram-ellenállás adott, akkor bármelyikből kiszámítható a hiányzó harmadik mennyiség és a teljesítmény. A következő formulák az Ohm-törvény segítségével levezetett kiszámítási módokat mutatják meg.

a) Ha az ellenállás és az áramerősség ismert:

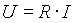
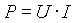
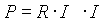
átrendezve:

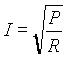
b) Adott ellenállás és feszültség esetén.

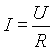
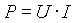
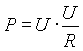
átrendezve:

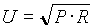
A bekeretezett formulát érdemes jól megjegyezni.

Negyedik gyakorlat:

Egy HF kimenőteljesítmény mérése alkalmával 100 V feszültséget mérünk az 50 ohm-os ellenálláson.
Mekkora teljesítmény jön ki az adóból?

A) 5 kW B) 500 W C) 200 W D) 2 W

A villamos munka

Akár csak a mechanikában, a villamos munka jelölésére a W-t (angol Work szóból) használjuk legtöbbször. A munka a hosszabb ideig tartó egyenletes teljesítményt jelenti.

W = P*t; munka = teljesítmény*idő

A következő összefüggés megadja a villamos munkára vonatkozó legfontosabb összefüggést.

Ha a képletbe voltban, ampernem és másodpercben helyettesítjük az adatokat, akkor végül VAs-ot, vagy más néven Ws-ot (wattszekundum) kapunk.

Megjegyzés: A munka alapegysége a Ws. De ez viszonylag kicsi egység, így sokszor használjuk helyette a kWh-t (kilowattóra).

Ötödik gyakorlat:

Hány Ws egy kWh?

Megjegyzés: Az órát szekundumban kell behelyettesíteni!

A) 3 600 000 Ws B) 60 000 Ws C) 3 600 Ws D) 60 Ws

Erre az átváltásra szükség lehet, amikor a villamos energiáért fizetendő összeget számoljuk. Az áramszolgáltató felé a villamos munkáért fizetünk, nem pedig a teljesítményért. Fontos, hogy a teljesítményt mennyi ideig vettük fel a hálózatból.

Példa:

Egy számítógép 120 W teljesítményt vesz fel a hálózatból.

• a) Mekkora a napi energiafogyasztás (villamos munka kWh-ban), ha a gép minden nap 8 és 18 óra között üzemel?
• b) Mennyibe kerül a napi üzemeltetéssel elhasznált energia, ha egy kWh 40 Ft?

Megoldás:

• a) W = P*t = 120 W × 10 h = 1200 Wh = 1,2 kWh
• b) Költség: K = 1,2 kWh × 40 Ft/kWh = 48 Ft

Tehát a napi üzemeltetés 48 forintba kerül. Ezek szerint, ha valaki napi 10 órán át üzemeltet egy ilyen számítógépet, akkor az havonta közelítőleg 1500 forintba, azaz 6 euroba kerül.

Tesztfeladatok

A fejezethez tartozó feladatok segítik a felkészülést a rádióamatőr vizsgára. A következő példákkal gyakorlatot szerezhetünk az Ohm-törvény, teljesítmény és munka számításában.

TB504*) A villamos teljesítmény mértékegysége a ...

A) joule. B) amperóra. C) kilowattóra. D) watt.

TB506 A következők közül melyik a helytelen összefüggés?

A	B	C	D

TB507 Mekkora feszültség hatására folyik 2 A egy 50 ohm-os ellenálláson?

A) 25 V B) 52 V C) 100 V D) 200 V

TB508 Mekkora ellenálláson folyik 3 A a rákapcsolt 90 V feszültség hatására?

A) 1/30 ohm B) 30 ohm C) 93 ohm D) 270 ohm

TB525 Melyik az a sor, amelyikben mindkét összefüggés helyes?

A
B
C
D

TB526 Melyik az a sor, amelyikben mindkét összefüggés helyes?

A
B
C
D

TB527 Egy energiaforrás 230 V mellett 0,63 A-t szolgáltat. Mekkora munkát végez a forrás, ha 7 órán át ilyen paraméterekkel üzemel?

A) 0,1 kWh B) 1,015 kWh C) 2,56 kWh D) 20,7 kWh

TC500 Egy 10 kohm-os ellenállás maximális terhelhetősége (max. teljesítménye) 1 W. Mekkora az a legnagyobb feszültéség, amit az ellenállás károsodás nélkül elvisel?

A) 3,16 V B) 31,6 V C) 10 V D) 100 V

TC501 Egy 120 ohm-os ellenállás maximális terhelhetősége 23 W. Mekkora az a legnagyobb áram, amit az ellenállás károsodás nélkül elvisel?

A) 19,2 mA B) 192 mA C) 43,7 mA D) 437 mA

Megoldások

A fejezet folyamán előforduló gyakorlatok megoldásai:

Első gyakorlat:

R (kOhm)	2	4	8
I (mA)	12	6	3

• Második gyakorlat: B
• Harmadik gyakorlat: C
• Negyedik gyakorlat: C
• Ötödik gyakorlat: A

A helyes megoldások részletei a következő linken találhatók: Függelék

Tesztfeladatok

A következő táblázatban a feladat számára kattintva megtekinthetők a megoldások.

TB504

TB506

TB507

TB508

TB525

TB526

TB527

TC500

TC501

TC517

Legalább 7 feladatot sikerült megoldani? Az elég. Ezek a példák a vizsgafeladatokhoz hasonló nehézségűek voltak.

© http://tankonyv.ham.hu, utolsó módosítás: 2023.09.03. 00:30
Eredeti mű: © Eckart Moltrecht DJ4UF, http://www.amateurfunkpruefung.de